回帰モデルにおけるL1正則化とL2正則化の効果
概要
回帰モデルとは、与えられた入力を用いて目標変数
を予測するモデルです。
回帰モデルでは過学習を防ぐため、誤差関数(二乗誤差関数など)に次の式で表される正則化項を加えて最小化します。
この形の正則化項を用いる回帰をブリッジ回帰と呼びます。
特にの時をLasso回帰、
の時をRidge回帰と呼びます。また、それぞれに用いられている正則加項をL1ノルム、L2ノルムと呼びます。
L1ノルムとL2ノルムの特徴を簡単にまとめると次のようになります。
- L1ノルムはパラメータの一部を完全に0にするため、モデルの推定と変数選択を同時に行うことができる
- 特に次元数>>データ数の状況で強力
- L2ノルムは微分可能であり解析的に解けるが、L1ノルムは 解析的に計算出来ない
- L1ノルムには様々な推定アルゴリズムが提案されている
また、L1ノルムには
- 次元
が標本数
より大きい時、高々
個の変数までしか選択できない
- 説明変数間に強い相関がある場合、相関を捉えきれず適切な変数選択が行われるとは限らない
といった問題があり、これを解決するために、L1ノルムとL2ノルムを線形結合したElastic Netというモデルも提案されています。
Elastic NetはRidge回帰とLasso回帰の両方の性質を有しています。
こういった特徴が実際にはどのような結果として表れるか、多項式回帰を用いて実験してみました。
コード
今回はPythonのscikit-learnという機械学習ライブラリを用いて実験しました、
コードは次のリンクにあります。
Regularization by Bridge Regression
実験
データの生成に用いた関数は次式になります。
この関数にに従う乱数を加えたデータ20個を用いました。
結果は次のようになりました。
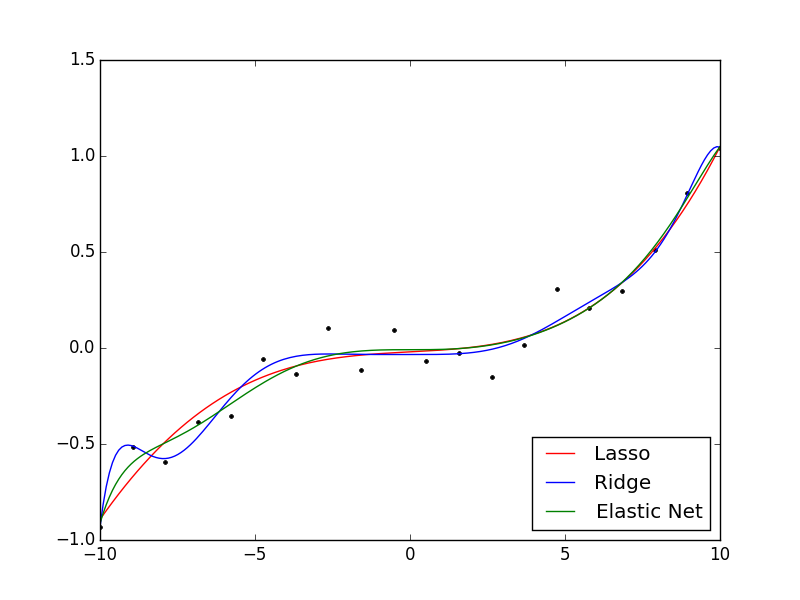
今回の場合、L2ノルムを用いた場合は若干過学習気味に、L1ノルムを用いた場合は正則化の効果が程よく得られてる印象を受けます。Elastic NetはL1とL2の中間くらいのモデリングになっています。
パラメータの値は以下のようになっています。
| Lasso | Ridge | Elastic Net | |
|---|---|---|---|
| 0 | 0 | 0 | |
| 8.46E-03 | -5.55E-06 | 0 | |
| 0 | 9.18E-06 | 0 | |
| 8.86E-04 | 2.85E-04 | 1.63E-03 | |
| 7.47E-06 | 4.54E-04 | -8.58E-05 | |
| 0 | 6.34E-05 | -9.49E-06 | |
| 2.33E-08 | -2.33E-05 | 1.70E-06 | |
| 0 | -1.22E-06 | -4.91E-08 | |
| 0 | 3.69E-07 | 3.67E-09 | |
| 0 | 6.53E-09 | 7.88E-10 | |
| 0 | -1.80E-09 | -1.14E-10 |
L1ノルムは確かにパラメータの一部が完全に0になっていることが確認されました。
また、Elastic Netも一部変数が0になっています。
考察
L2ノルムが過学習を起こしてる理由としては学習データが非常に少ないからであり、これは各正則化の差を見るために意図的に少なくしています。
他のデータも用いて実験してみたのですが、常にどのノルムが一番優れている、ということはほとんどないようです。
Sin関数に従うデータを用いた実験も行ってみましたが、Elastic Netが一番当てはまりがよく、次にL2ノルム、L1ノルムといった感じでした。(あくまで見た目での判断ですが)
L1ノルムはパラメータが0になりやすく、正則化の影響が非常に強いと感じられました。
対してL2ノルムは過学習になりやすく、正則化の影響が少し弱いと感じられました。
Elastic Netは当てはまりの良いモデルとなることが多かったと思います。
今回は低次元の多項式回帰での実験ですが、L1ノルムの真価は高次元での線形回帰で発揮されると思うので、そちらに関しても今度実験してみようと思います。
参考
川野秀一, et al. "回帰モデリングと L1 型正則化法の最近の展開." 日本統計学会誌 39.2 (2010): 211-242.
http://svr4.terrapub.co.jp/journals/jjssj/pdf/3902/39020211.pdf
回帰モデルの正則化について詳しく扱っています。
MacでPythonの機械学習環境構築(2015年2月版)
概要
MacでPythonの管理と機械学習環境構築の備忘録です。
2015年2月版です。
簡単にまとめるとこんな感じです。
前回は結構めんどくさかったのですが、各ライブラリのバージョンアップのお陰でかなり簡単にインストールできるようになりました。
前準備
バージョン管理システムはhomebrewを使います。
パッケージ管理システムとは、ソフトウェアをまとめて管理(インストールやアップデート、削除等)するためのソフトです。
homebrewについては次の解説が参考になります。
- 公式
Homebrew — The missing package manager for OS X
- インストール、使い方
MacOSX - パッケージ管理システム Homebrew - Qiita
# homebrewのインストール ruby -e "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/master/install)"
Pythonの導入・管理
Pythonの管理には、pyenvを使います。
yyuu/pyenv · GitHub
pyenvは、Pythonをバージョンごとに個別に管理するためのソフトです。
非常にややこしいPythonの環境構築を簡単にしてくれます。
# pyenv のインストール brew install pyenv
pyenvを使う前に環境変数を設定する必要があります。
.bash_profileに次のコマンドを書き足します。
# 環境変数の設定 export PATH="$HOME/.pyenv/shims:$PATH"
pyenvは様々なバージョンのPython(やサードパーティ)に対応しています。
次のコマンドでインストールできるPythonの種類を確認できます。
# pyenvでインストールできるPythonの確認 pyenv install -l
例えば、(2015年2月時点で)最新版のPython 3.4.2は、
pyenv install 3.4.2
でインストールできます。
デフォルトではユーザディレクトリの.pyenv以下にインストールされます。
機械学習ライブラリの構築
Pythonの機械学習ライブラリとして、Anacondaを使います。
Anaconda Scientific Python Distribution
- numpy
- scipy
- matplotlib
- scikit-learn
- pandas
あたりが定番なのですが、Anacondaはこれらをひとまとめにしてインストールしてくれます。個別にインストールするよりすごい楽です。iPython等の開発に便利なツールもインストールしてくれます。
Anacondaはpyenvでインストールできます。
2015年2月現在、AnacondaはPython2系のパッケージとPython3系のパッケージがあります。
Python 2系を使っている方は anaconda-2.1.0 を、Python3系を使っている方は anaconda3-2.1.0 をインストールしてください。
# Anacondaのインストール # 数百Mあるので結構時間かかります。10分くらい? # バージョンは適宜最新版に書き換えてください # Python2をベースにしたパッケージ # Python2で仕様したい方はこちらをインストールしてください pyenv install anaconda-2.1.0 # Python3をベースにしたパッケージ # Python3で仕様したい方はこちらをインストールしてください pyenv install anaconda3-2.1.0
以降の説明はPython3系を元に行います。
インストールしたらおまじない(再ハッシュ)しましょう。
pyenv rehash
pyenvでは使用するバージョンのPythonを選択できます。
先程インストールしたAnacondaに設定する場合は、
# 使用するPythonの選択 pyenv local anaconda3-2.1.0 pyenv global anaconda3-2.1.0
といった感じです。
ローカル環境とグローバル環境で使い分けられます。が、とりあえずは両方同じPythonに設定しておきます。
余談
pyenvでよく使うコマンドは
# 現在使ってるPythonの確認 pyenv version # インストールされてるPythonの確認 pyenv versions # Pythonのアンインストール pyenv uninstall
あたりです。詳しくはここに。
pyenv/COMMANDS.md at master · yyuu/pyenv · GitHub
Pythonに関して言えば、一つのPythonをアップデートして使うより、バージョンごとに新しくPythonの環境を構築したほうが良いと思います。*1
ディリクレ過程ガウス混合モデルの Python 実装(「続・わかりやすいパターン認識」ノート)

- 作者: 石井健一郎,上田修功
- 出版社/メーカー: オーム社
- 発売日: 2014/08/26
- メディア: 単行本(ソフトカバー)
- この商品を含むブログ (2件) を見る
「続・わかりやすいパターン認識」12章のディリクレ過程ガウス混合モデル(DPGMM)を Python で実装してみました。
コードはこちら。
http://nbviewer.ipython.org/github/breakbee/PyNote/blob/master/Implementation_of_DPGMM.ipynb
参考
wishart and inverse wishart sampler
ウィシャート分布 - MATLAB & Simulink - MathWorks 日本
掲載されているアルゴリズムでは、
という3つのステップを何度も繰り返し、事後確率が収束すれば終了、というアルゴリズムですが、今回は簡単のため、ステップ1と2を繰り返すことにしています。
(つまり、事後確率が大きくなるにしろ小さくなるにしろ潜在変数とパラメータを更新しています。)
実際にDPGMMを適用した結果はこんな感じになりました。(初期クラスタ数は1に設定)

ちゃんと適切な混合数を選択できていることが確認できました。
実装していて分からなかったのですが、CRPで潜在変数をサンプリングしている時、新しくクラスタが増えた場合、そのクラスタのパラメータも同時に生成する必要があると思うのですが、基底測度(というか事前分布)からサンプリングすれば良いのでしょうか?
とりあえず適当に初期化したパラメータを新規クラスタに与えたところ、一応期待通りの動作をしているのですが、あまり厳密ではないかもしれません...
ともあれ、DPGMM自体は130行くらいで実装できたので、結構シンプルに書けるものだなと思いました。(式の導出はとても大変でしたが)
【書評】続・わかりやすいパターン認識 -教師なし学習入門-

- 作者: 石井健一郎,上田修功
- 出版社/メーカー: オーム社
- 発売日: 2014/08/26
- メディア: 単行本(ソフトカバー)
- この商品を含むブログ (2件) を見る
概要
「続・わかりやすいパターン認識 -教師なし学習入門-」の書評です。
本書は「教師なし学習」について、基礎から応用、最先端の内容までまとめた一冊です。
タイトルに「続」とあるように、「わかりやすいパターン認識」の続編という位置づけですが、前作を読んでいなくても理解できるような構成になっています。

- 作者: 石井健一郎,前田英作,上田修功,村瀬洋
- 出版社/メーカー: オーム社
- 発売日: 1998/08
- メディア: 単行本
- 購入: 19人 クリック: 110回
- この商品を含むブログ (40件) を見る
内容
最初の3分の1が統計的な知識などの基礎的な内容です。
統計・ベイズ統計についての説明と、それらを用いたパラメータ推定について説明しています。
次の3分の1が応用的、というかメジャーな教師なし学習アルゴリズムに関する内容です。
EMアルゴリズム、隠れマルコフモデル、ガウス混合モデル、K-Means、凸クラスタリングといった内容を扱います。
教師あり学習と教師なし学習を常に対比させながら説明が進むので、この2つがどう違うのかということをきっちり理解できると思います。
最後の3分の1が最先端の内容、ノンパラメトリックベイズに関するものです。
本書では70ページ以上使ってノンパラメトリックベイズの基礎から応用まで丁寧に説明しています。
ノンパラメトリックは初心者向けのまとまった資料がほとんどない状況だったので、非常に価値のある内容ではないかと思います。
良いところ
特に良いと思ったのは、
- 読者が数式をしっかり追えるように細かい配慮がなされていること
- 具体的な実験例が豊富で理解しやすいこと
の二点です。タイトルにある「わかりやすい」は、「理解しようと努力した時に手助けしてくれる」という意味だと思います。
また、説明の切り口が独特な箇所がいくつかあり、すでに知っている内容についても再発見がありました。
機械学習を初めて勉強する人におすすめの入門書
概要
私が機械学習の勉強を始めた頃、何から手を付ければ良いのかよく分からず、とても悩んだ覚えがあります。同じような悩みを抱えている方の参考になればと思い、自分が勉強していった方法を記事にしたいと思います。
目標としては、機械学習全般について、コンパクトなイメージを持てるようになることです。
そのためにも、簡単な本から始めて、少しずつ難しい本に挑戦して行きましょう。
入門書
何はともあれ、まずは機械学習のイメージを掴むことが大切です。
最初の一冊には、フリーソフトでつくる音声認識システムがおすすめします。

フリーソフトでつくる音声認識システム - パターン認識・機械学習の初歩から対話システムまで
- 作者: 荒木雅弘
- 出版社/メーカー: 森北出版
- 発売日: 2007/10/17
- メディア: 単行本(ソフトカバー)
- 購入: 45人 クリック: 519回
- この商品を含むブログ (38件) を見る
この本は二部構成なのですが、第一部に機械学習についての簡潔なまとめがあり、これがとても良くまとまっています。(第二部が音声認識についてです。)
必要な数学レベルも高校程度なので、簡単に読めるのではないかと思います。
機械学習に関する簡単なイメージを持てたら、機械学習を全般的に扱っている入門書に進みましょう。
二冊目には、はじめてのパターン認識をおすすめします。

- 作者: 平井有三
- 出版社/メーカー: 森北出版
- 発売日: 2012/07/31
- メディア: 単行本(ソフトカバー)
- 購入: 1人 クリック: 7回
- この商品を含むブログ (2件) を見る
本書では機械学習に関するトピックを幅広く扱っていて、話の進み方や式の導出等、わかりやすく進んでいきます。一冊目よりは数学の知識が必要になって来ますので、もし数式で躓いたら数学書(後述)を随時参考すると良いと思います。
この本を使って勉強会をしたことがあるのですが、特に
の3つがつまずきやすいポイントのようです。私もここでつまずきました。
最尤推定について、まず尤度が良く分からない、という意見が多かったです。
尤度については次の記事が分かりやすいのではないかと思います。
尤度とは何者なのか? - MY ENIGMA
主成分分析は線形代数の分野なので、後述するキーポイント線形代数を読んでから勉強すると理解しやすいと思います。
EMアルゴリズムについては、東京工業大学の杉山先生の解説が分かりやすいのではないかと思います。
情報認識 - TOKYO TECH OCWの第10回です。
三冊目には、二冊目でカバーできなかったところを中心に解説してる本をオススメします。
データ解析のための統計モデリング入門は、見かけこそごついですが、とても説明が丁寧で分かりやすい本です。

データ解析のための統計モデリング入門――一般化線形モデル・階層ベイズモデル・MCMC (確率と情報の科学)
- 作者: 久保拓弥
- 出版社/メーカー: 岩波書店
- 発売日: 2012/05/19
- メディア: 単行本
- 購入: 16人 クリック: 163回
- この商品を含むブログ (19件) を見る
「はじめてのパターン認識」でも確率モデルの話題があったように、機械学習の分野では統計学が大きな役割を果たします。本書ではそこを重点的に学びます。
この本で扱っているモデルを一般に「生成モデル」と呼びます。(「はじめてのパターン認識」で扱っていた、線形識別関数やSVM等は、「識別モデル」と呼ばれています。)
また、この本では主に「回帰」問題を、「はじめてのパターン認識」では主に「分類」問題を扱っています。*1そういった意味でバランスが取れているのではないかと思います。*2
この本を読むにあたって、確率や統計学の知識があったほうが読みやすいと思います。後述する統計関連の本(後述)を随時参考すると良いと思います。
数学の入門書
機械学習の分野では、微積や線形代数など、様々な数学が必要になって来ます。
数学については人によって事前の理解度が異なると思いますので、勉強中に数式に引っかかるようになって来たら、数学書を参照すると良いでしょう。
私のオススメはキーポイントシリーズです。

- 作者: 薩摩順吉,四ツ谷晶二
- 出版社/メーカー: 岩波書店
- 発売日: 1992/10/22
- メディア: 単行本
- 購入: 5人 クリック: 30回
- この商品を含むブログ (26件) を見る

- 作者: 川村清
- 出版社/メーカー: 岩波書店
- 発売日: 1996/03/28
- メディア: 単行本
- 購入: 1人 クリック: 3回
- この商品を含むブログ (2件) を見る
レビュー : 「パターン認識と機械学習」への遠回り その4 「キーポイント線形代数」 - old school magic
特にキーポイント線形代数は、数ある線形代数の入門書の中でも、イメージしやすいという点で良書だと思います。
また、本書もトピック毎によくまとまっていてオススメです。

- 作者: 永田靖
- 出版社/メーカー: 朝倉書店
- 発売日: 2005/04/01
- メディア: 単行本
- 購入: 23人 クリック: 398回
- この商品を含むブログ (23件) を見る
統計学の入門書
統計学は機械学習において重要なのですが、機械学習の本の中で統計学をしっかり説明するだけの余白はありません。
ならばいっそのこと、統計学そのものをしっかり学んでいきましょう。
次の二冊は、統計学の入門書の入門書、といったレベルですが、機械学習の本を理解する上で確実に役に立ちます。

- 作者: 和達三樹,十河清
- 出版社/メーカー: 岩波書店
- 発売日: 1993/02/22
- メディア: 単行本
- 購入: 1人 クリック: 38回
- この商品を含むブログ (5件) を見る

図解・ベイズ統計「超」入門 あいまいなデータから未来を予測する技術 (サイエンス・アイ新書)
- 作者: 涌井貞美
- 出版社/メーカー: SBクリエイティブ
- 発売日: 2013/12/18
- メディア: 新書
- この商品を含むブログ (10件) を見る
自然言語処理
自然言語処理においても、機械学習が用いられています。特に、離散値や系列データを扱うので、今まで読んできた本(連続値や非系列データ)とは違う視点から勉強ができると思います。

- 作者: 高村大也,奥村学
- 出版社/メーカー: コロナ社
- 発売日: 2010/07
- メディア: 単行本
- 購入: 13人 クリック: 235回
- この商品を含むブログ (39件) を見る
パターン認識と機械学習(通称PRML)
これまで学んできたことで、浅く広くではありますが、機械学習全般について学べたと思います。
ここから更に詳しいこと、またまだ学んでいないことを学ぶ時、PRMLが一つの選択肢になると思います。

- 作者: C.M.ビショップ,元田浩,栗田多喜夫,樋口知之,松本裕治,村田昇
- 出版社/メーカー: 丸善出版
- 発売日: 2012/04/05
- メディア: 単行本(ソフトカバー)
- 購入: 6人 クリック: 33回
- この商品を含むブログ (14件) を見る

- 作者: C.M.ビショップ,元田浩,栗田多喜夫,樋口知之,松本裕治,村田昇
- 出版社/メーカー: 丸善出版
- 発売日: 2012/02/29
- メディア: 単行本
- 購入: 6人 クリック: 14回
- この商品を含むブログを見る
PRMLはものすごく難しいですし、少なくとも最初に読む本ではありませんが、間違いなく良書です。特に、ベイズ理論を用いた機械学習という点においては、本書が最も良いのではないかと思います。
機械学習への理解を深めたい時、気長に読み進めると良いと思います。
PRMLは式変形の省略が多いので、次の副読本と一緒に読むことをおすすめします。

パターン認識と機械学習の学習―ベイズ理論に挫折しないための数学
- 作者: 光成滋生,竹迫良範
- 出版社/メーカー: 暗黒通信団
- 発売日: 2012/07
- メディア: 単行本
- 購入: 8人 クリック: 228回
- この商品を含むブログ (7件) を見る
同書はGithubでも公開されています。
https://github.com/herumi/prml
まとめ
機械学習は広大な分野です。最初から全てを理解しようとせず、各トピック毎にコンパクトなイメージを持ちつつ、知識を上塗りして行くのが良いと思います。
また、実際にプログラミングしてみるのも良いと思います。
RやPython、Matlab等が機械学習や統計において良く使われています。好きな言語で、ライブラリ等を用いて実際に機械学習してみるだけでも理解が深まります。また、アルゴリズムを実装してみるのも理解の助けになるでしょう。
多変量解析や時系列解析など、ここにある本だけではカバーしきれなかったトピックもたくさんあります。また、学習理論といった理論的な部分に挑戦してみるのもいいと思います。数学や統計の知識ももっとたくさん必要になってくるでしょう。正直私もここからが大変な気がしています。頑張ります。
「パターン認識と機械学習」への遠回り その7 「データ解析のための統計モデリング入門」

データ解析のための統計モデリング入門――一般化線形モデル・階層ベイズモデル・MCMC (確率と情報の科学)
- 作者: 久保拓弥
- 出版社/メーカー: 岩波書店
- 発売日: 2012/05/19
- メディア: 単行本
- 購入: 16人 クリック: 163回
- この商品を含むブログ (21件) を見る
機械学習の分野では統計学が大きな役割を果たします。
この本では生態学のデータ解析をテーマに、統計モデリングを一から学んでいきます。
ハードカバーでちょっと難しそうに見える本ですが、内容はかなり初学者向けで、分かりやすく書かれていると思います。
一般化線形モデルから始まり、統計学のあれこれを説明しつつ、階層ベイズモデルやMCMCといったベイズ関連の手法へと進んでいきます。
良いところ
説明が非常に丁寧な本です。
統計学は独学だとちょっと雲を掴むような感じがして勉強し辛いところがあるのですが、この本では理解度のフローチャートや、章ごとの内容のまとめなど、勉強の助けになる要素が散りばめられています。
統計学やベイズ統計への「一歩進んだ」入門書としては最適なのではないかと思います。
気になったところ
本書は基本的にR言語とMCMCソフトとしてWinBUGSを用いているので、他言語のユーザは読み替える必要があると思います。
MCMCソフトとしては他にはStan等が有名どころだと思います。
本書に出てくるWinBUGSコードをStanコードに書き換えた方のリンク等がサポートページに掲載されています。
サポートページ
http://hosho.ees.hokudai.ac.jp/~kubo/ce/IwanamiBook.html
私のブログでもPythonを用いて本書に関する事(一般化線形モデルとMCMC)をいくつか試しているので、よろしければどうぞ。
Pythonで一般化線形モデル - old school magic
PyMC3でMCMC入門(1) - old school magic
PyMC3でMCMC入門(2) - old school magic
PyStanでMCMC入門 - old school magic
今まで読んだ本
「パターン認識と機械学習」への遠回り その1 「フリーソフトでつくる音声認識システム」 - old school magic
「パターン認識と機械学習」への遠回り その2 「自然言語処理のための機械学習入門」 - old school magic
「パターン認識と機械学習」への遠回り その3 「はじめてのパターン認識」 - old school magic
「パターン認識と機械学習」への遠回り その4 「キーポイント線形代数」 - old school magic
「パターン認識と機械学習」への遠回り その5 「キーポイント確率・統計」 - old school magic
「パターン認識と機械学習」への遠回り その6 「図解・ベイズ統計「超」入門」 - old school magic
PyStanでMCMC入門
概要
PyStan は Stan というMCMC計算用言語の Python インターフェイスです。
Stan
http://mc-stan.org/
PyStan
http://pystan.readthedocs.org/en/latest/index.html
MCMCを計算できるソフトはいくつかあるのですが、Stan は
- C++で実装されているため高速
- 最近のサンプリング法を実装している
といった特徴があります。特に速度には目を見張るものがあります。
前回までは PyMC3 をいじっていたのですが、他のソフトにも触ってみようと思い、今回は PyStan でモデリングをしてみました。
PyStan のインストール
Anaconda を入れればもれなく一緒にインストールされます。
Anaconda
https://store.continuum.io/cshop/anaconda/
参考
MacでPythonの機械学習環境構築(2014年5月版) - old school magic
もしくは pip でインストールします。
pip install pystan
参考
http://pystan.readthedocs.org/en/latest/getting_started.html
(※追記 Anacondaだとデフォルトで入ってませんでした... pip でインストールするのが正解ですね)
データの生成
今回モデリングするのは、ガウス混合モデルというモデルです。
その名の通りいくつかのガウス分布を混合したモデルで、今回は3個の1次元ガウス分布を混合しています。
まずは真の分布からデータを生成します。
import pystan import numpy as np import matplotlib.pyplot as plt mean1 = 10 mean2 = -10 mean3 = 0 num1 = 200 num2 = 300 num3 = 500 X = np.concatenate([ np.random.normal(loc=mean1, scale=1, size=num1), np.random.normal(loc=mean2, scale=1, size=num2), np.random.normal(loc=mean3, scale=1, size=num3) ]) np.random.shuffle(X)
真の平均はそれぞれ、真の混合比は
です。標準偏差は簡単のため全て1としています。
ヒストグラムにするとこんな感じのデータです。

このデータを用いてMCMCサンプリングを行い、平均と混合比の事後分布を推定する、というのが今回の目的です。
Stan によるモデリング
PyStan は Stan言語のインターフェイスなので、Stan言語でモデリングを行い、Pythonから呼び出します。
今回のガウス混合モデルのモデリングはこんな感じです。これを gmm_mcmc.stan というファイル名で保存します。
data {
int<lower=1> N;
int<lower=1> k;
real X[N];
}
parameters {
simplex[k] theta;
real mu[k];
}
model {
real ps[k];
for (i in 1:k){
mu[i] ~ normal(0, 1.0e+2);
}
for(i in 1:N){
for(j in 1:k){
ps[j] <- log(theta[j]) + normal_log(X[i], mu[j], 1.0);
}
increment_log_prob(log_sum_exp(ps));
}
}Stan はC言語のような手続き型の言語です。Pythonとは異なりコードブロックを用いています。
Stan には、基本的に次の4つのブロックがあります。
- data
- parameters
- transformed parameters
- model
data ブロックは用いるデータを宣言しておくブロックです。
このブロックにPythonなどのインターフェイスからデータを渡すことになります。
今回は、データと、データのサイズと、混合数を渡しています。
parameters ブロックはモデルのパラメータを宣言するブロックです。
今回の例で言えば、平均 mu と混合比 theta です。
theta の型である simplex というのは、ディリクレ分布を事前分布に設定した時に使う特別な型です。(後述)
transformed parameters ブロックは、parameters ブロックで宣言したパラメータを用いて新しいパラメータを定義するブロックです。
今回は用いていませんが、例えばというパラメータがあった時、
などと宣言します。
model ブロックは、モデルを記述するブロックです。
モデルの記述方法には、
- Log Probability Increment
- Sampling Statement
の2種類があります。
平均 mu のサンプリングには Sampling Statement を用いています。
for (i in 1:k){
mu[i] ~ normal(0, 1.0e+2);
}このように、~ の左側にパラメータ、右側に従う分布を描く方法です。
(モデルの)平均の事前分布には、平均0、標準偏差100の正規分布を用いています。
混合比 theta のサンプリングには Log Probability Increment を用いています。
real ps[k];
for(i in 1:N){
for(j in 1:k){
ps[j] <- log(theta[j]) + normal_log(X[i], mu[j], 1.0);
}
increment_log_prob(log_sum_exp(ps));
}対数をとった確率(Log Probability)の式を記述することによって計算を行う方法です。
基本的にどちらの記述を用いても良いのですが、前述した simplex 型、つまり混合比の事前分布であるディリクレ分布に従うパラメータは、制約上 Log Probability Increment でしか記述できないようです。
参考
マニュアル(pdf)
https://github.com/stan-dev/stan/releases/download/v2.4.0/stan-reference-2.4.0.pdf
- 9.2(混合分布について)
- 21.3(モデルの記述方法について)
- 44(simplex 型について)
PyStan からの呼び出し
では、この Stan によるモデリングを Python から呼び出してみましょう。
N = X.shape[0]
k = 3
stan_data = {'N': N, 'k': k, 'X': X}
fit = pystan.stan(file='gmm_mcmc.stan', data=stan_data, iter=10000, chains=1)
print('Sampling finished.')
# 可視化
fit.plot()
plt.show()Python側からデータを渡す時、Stan の data ブロックで宣言した名前をキーにした辞書型にして渡します。
今回の例でいうところの stan_data です。データ数と混合数、データを辞書にして渡しています。
今回のサンプリングでは、サンプリング回数(iter)は10000回、サンプリング系列数(chains)は1としています。(通常は複数のサンプリングを走らせます。)
そのうち最初の5000回(ちょうど半分)は burn-in という処理の対象となります。簡単にいうと、サンプリングの最初の方は精度が悪いので捨てます。この捨てる数はもちろん調整可能です。(デフォルトで半分。)
サンプリングの結果はこんな感じです。

混合比も平均も、おおよそ真値を中心にうまく分布しているのが見て取れますね。
サンプリング系列数(chains)を4にするとこんな感じです。

今回使用したコードはこちらです。(Gist)
PyStan Code
PyStan Code for GMM
Stan Code
Gaussian Mixture Model for Stan
感想
PyMC と比べて、PyStan は高速だけど記述が面倒、といった印象を受けました。
PyMC3 は少しバグが多いので、マニュアルがしっかりしてて安定してる Stan は魅力的でした。
しかし、PyMCに比べて記述量が増えるので、Stan言語の記述に慣れるかどうかが1つのポイントかもしれません。
書いててC言語を思い出しました。
PyStan の日本語資料はあまりなかったのですが、 RStan は結構ありました。
両方 Stan のインターフェイスで、Stanコードは共通なので、割りと調べやすかったです。
参考資料
公式の入門手引きの解説もとてもわかり易いです。
PyStan Getting started
http://pystan.readthedocs.org/en/latest/getting_started.html
PyStan の貴重な日本語の活用事例です。
Pystanで自然言語処理 scikit.learnのdatasetで試す - xiangze's sparse blog
マニュアルも非常に細かく書かれています。
https://github.com/stan-dev/stan/releases/download/v2.4.0/stan-reference-2.4.0.pdf
日本語でマニュアルの解説をしている方の記事です。
Stanのマニュアルの8章~12章の私的メモ
Stan のチュートリアルを作成してくださった方のスライドです。
http://www.slideshare.net/teitonakagawa/stantutorialj