2014-08-09

PyMC3でMCMC入門(2)

Python 機械学習統計

概要

前回は、PyMC2 向けのチュートリアルを PyMC3 に書き換えることでPyMC3 に入門してみました。
今回は、PyMC3 のチュートリアルを見て、実際にモデルを記述する時どういった流れになるか見てみようと思います。

チュートリアル

PyMC3 チュートリアル
http://nbviewer.ipython.org/github/pymc-devs/pymc/blob/master/pymc/examples/tutorial.ipynb

このチュートリアルを頭から見てみましょう。
まずはサンプルの生成です。

import pymc as pm
import numpy as np

ndims = 2
nobs = 20

xtrue = np.random.normal(scale=2., size=1)
ytrue = np.random.normal(loc=np.exp(xtrue), scale=1, size=(ndims, 1))
zdata = np.random.normal(loc=xtrue + ytrue, scale=.75, size=(ndims, nobs))

${x_{true}}$ は ${N(0, 2^2)}$ 、つまり平均0、標準偏差2の正規分布の1次元正規分布に従う1つの値です。
${y_{true}}$ は ${N(exp(x_{true}), 1)}$ 、つまり平均 ${exp(x_{true})}$ 、標準偏差1の正規分布の1次元正規分布に従う2つの値です。サンプリングされた2つの値を並べて2次元ベクトルとしています。
仮に ${y_{true} = (y_1, y_2)}$ とします。

${z_{data}}$ は ${N((x_{true}+y_1, x_{true}+y_2), 0.75)}$ つまり平均 ${(x_{true}+y_1, x_{true}+y_2)}$ 、共分散行列が単位行列の0.75倍である2次元正規分布に従う20個の値です。

今回の実験では、 ${x_{true} = -2.99736635, y_{true} = (-0.21840065, -0.53160934)}$ という値が得られました。

次にモデリングを見てみましょう。

with pm.Model() as model:
    x = pm.Normal('x', mu=0., sd=1)
    y = pm.Normal('y', mu=pm.exp(x), sd=2., shape=(ndims, 1))
    z = pm.Normal('z', mu=x + y, sd=.75, observed=zdata)

今回の目的は、この ${z_{data}}$ が得られていて、 ${N((x+y_1, x+y_2), 0.75)}$ というモデルに従っていると仮定した時、 ${x}$ と ${y}$ の事後分布を計算することです。
この事後分布が真の値を中心に広がっていれば成功、ということです。

${x}$ と ${y}$ がどんな分布に従っているかは分からないので、とりあえずそれぞれ

${x}$ : 平均0、標準偏差1の正規分布
${y}$ : 平均 ${exp(x)}$ 、標準偏差2の正規分布

を事前分布として仮定します。
モデリングする側からすれば知りようのないことですが、真の分布とは異なる分布に従っていますね。

このモデルを用いてサンプリングを行うのですが、このチュートリアルではその初期値をMAP推定法(最大事後確率推定法)を用いて設定しています。

with model:
    start = pm.find_MAP()

print("MAP found:")
print("x:", start['x'])
print("y:", start['y'])

print("Compare with true values:")
print("ytrue", ytrue)
print("xtrue", xtrue)

出力はこんな感じです。

MAP found:
x: -1.3848882353856375
y: [[-1.90266947]
 [-2.02702944]]
Compare with true values:
ytrue [[-0.21840065]
 [-0.53160934]]
xtrue [-2.99736635]

最大事後確率推定法は、簡単に言えば最尤推定法に罰則を付けたものです。
真の値からは少しずれていますが、初期値としては良い感じ、だと思います。

では、サンプリングを行いましょう。

with model:
    step = pm.NUTS()

PyMC3 ではサンプラーの設定を行います。
NUTS は No-U-Turn Sampler の略で、最近考案されたサンプリング手法です。

with model:
    trace = pm.sample(10000, step, start)

今回は1種類ですが、変数毎にサンプラを設定することも可能です。

このサンプラーと初期値を用いて、10000回のサンプリングを行います。(チュートリアルでは3000回ですが増やしました。)

結果を可視化するとこんな感じになります。

f:id:breakbee:20140809210636j:plain

今回の結果だと、 ${x}$ は少し真値からずれたところを中心に分布していますが、 ${y}$ は真値に近いところを中心にしていますね。サンプルが20個と少ないので、もう少し増やせば精度も上がるのではないかと思います。
こんな感じで PyMC3 ではMCMCサンプリングを行います。

PyMC3 の長所と短所

PyMC3 の長所ですが、

Pythonだけでサンプリングを行える
モデルの記述が簡潔

というところだと思います。実際、

with pm.Model() as model:
    x = pm.Normal('x', mu=0., sd=1)
    y = pm.Normal('y', mu=pm.exp(x), sd=2., shape=(ndims, 1))
    z = pm.Normal('z', mu=x + y, sd=.75, observed=zdata)
    start = pm.find_MAP()
    step = pm.NUTS()
    trace = pm.sample(10000, step, start)

の7行でモデルの記述と初期値をサンプラーの設定、サンプリングを行えています。
実際に自分でモデルを記述する時も、このチュートリアルを書き換える形で進めることができるんじゃないかと思います。

PyMC3 の短所ですが、

サンプラの設定が面倒
まだまだバグが多い

といったところだと思います。
BUGS や Stan といったソフトだと、サンプラの設定は自動でしてくれるものが多いので、これがちょっと面倒かと思います。実際、モデルに合わないサンプラを使うと容赦なくバグがでます。

また、PyMC3 はアルファ版なのでまだまだバグが多いです。いくつか自分でもモデリングしてみたのですが、何個かバグに引っかかりました。(サンプリング時に初期値から動かない等)

Github の issue と stackoverflow にバグレポートが集まっているので、モデリングした時挙動がおかしかったら調べてみるといいのではないかと思います。

感想

PyMC3 はモデルの記述が簡潔で便利なのですが、まだまだバグも多いので、これからの発展に期待したいと思います。
Github の README にもあるように、初めて PyMC に触る方は PyMC2 のほうが安定してていいかもしれません。

次は PyStan について調べたことをまとめようかと思います。

2014-08-04

PyMC3でMCMC入門(1)

Python 機械学習統計

概要

先日、Tokyo.scipy というイベントがありました。

Tokyo.scipy

Python で科学技術計算を用いる方々の勉強会だそうです。
私は参加していないのですが、PyMC に関するセッションがあったそうです。

機械学習やデータマイニングで有名な神嶌先生の発表資料です。
非常に分かりやすいスライドでした。
このセッションで用いている PyMC は PyMC2 ですが、せっかくなので PyMC3 で書き換えてみました。PyMC3 の入門にちょうどいいのではないかと思います。

PyMC3 のインストール

こちらの記事をご参照ください。
Python3でPyMCのインストール - old school magic

サンプル1

サンプル1(単純なガウス分布の平均パラメータの推定)

単純なガウス分布の平均パラメータをMCMCで計算しています。
PyMC3 のコードはこちら。(コードが表示されなかったら更新してみてください)

This is PyMC3 version of http://nbviewer.ipython.o ...

PyMC2 のコードとの主な違いですが、

PyMC3 では with 構文の中でモデルを構築し、サンプリングを行っています。
モデルを構築する時、PyMC2 では観測変数は value に値を、 observed に観測変数かどうかのフラグを代入しますが、 PyMC3 では observed に直接変数を代入してます。
このコードでは、サンプリングの初期値として、MAP推定の結果を用いています。

MAP推定とは「最大事後確率推定」の略で、簡単に言うと最尤推定に罰則を付けたものです。(ベイズ推定とは異なります。)

詳しくはPyMC3のチュートリアルをご参照ください。
http://nbviewer.ipython.org/github/pymc-devs/pymc/blob/master/pymc/examples/tutorial.ipynb

結果を画像(result1.jpg)で保存してます。

といった感じです。

結果はこんな感じです。
f:id:breakbee:20140804024407j:plain

真の平均は1.0ですが、この結果だと0.94くらいを中心に分布してるように見えますね...
でも元のサンプルも0.9を中心に分布してるので大丈夫...だと思います。

サンプル2

サンプル2(1入力，1出力のガウス単純ベイズ)

簡単なナイーブベイズをMCMCで計算しています。
PyMC3 のコードはこちら。

This is PyMC3 version of http://nbviewer.ipython.o ...

PyMC2 との主な違いですが、

PyMC3 では deterministic デコレータがありません。

PyMC2 のコードでは、

@deterministic(plot=False)
def mu(y=y, mu0=mu0, mu1=mu1):
    out = np.empty_like(y, dtype=np.float)
    out[y == 0] = mu0
    out[y == 1] = mu1
    return out

として確定的なオブジェクトを扱っていましたが、 PyMC3では、pymc.Deterministic を使用します。

mu = pm.Deterministic('mu', mu0 * (1-y_sample) + mu1 * y_sample)

参考: What's @pm.deterministic in pyMC3?
https://github.com/pymc-devs/pymc/issues/434

一応等価なコードになっている...はずです。
PyMC2 のコードでは、y をそのまま計算に使えているのですが、PyMC3 ではこの y はそのまま使えません。
というのも、y は ObservedRV というデータ型で、ようするに観測変数なので計算に使う用途で設計されてないようです。
なので y に束縛してる y_sample を用いて、ついでにコードを簡潔にしました。

(もし間違ってたらご指摘ください。)

結果を画像(result2.jpg)で保存してます。

といった感じです。

結果はこんな感じです。
f:id:breakbee:20140804030324j:plain

各パラメータともに真値のまわりで分布しているように見えるので多分あってるはず...

感想

PyMC3 はまだ alpha 版ですし、ドキュメントもあまり整備されてないのでちょっと大変ですが、これからも頑張ってみようと思います。
あと、一応続きます。次は公式のチュートリアルの和訳と解説でもやろうかな...

最後に、神嶌先生、素晴らしい資料をありがとうございます。
もし問題があればお知らせください。

2014-07-27

LDAで日本語PDF分析

Java Python 機械学習

概要

最近、LDAを(pythonで)実装する機会がありました。
サンプリングを用いる実装だったので、Python等のスクリプト言語だとどうしても計算時間が問題になってしまいます(特に大規模なデータに対して)。
せっかくなのでコンパイル系の言語であるJavaで実装し直し、ついでに日本語PDFファイル(というか日本語論文)をLDAで分析してみました。

全体的な手順としては、

PDFからテキスト抽出
正規表現で日本語を抽出
Mecabで形態素解析
特徴語(今回は名詞)の選択
ストップワードの除去
LDAで分析

となっています。

分析に使ったLDAの実装やスクリプトはGithubにあります。
LDAのJava実装
https://github.com/breakbee/LDA4J
PDF分析のスクリプト
https://github.com/breakbee/PDFAnalysis

Python(>3)
Java(>1.6)
sh
mecab

を使用しました。

LDA

LDA(Latent Dirichlet Allocation)は、簡単に言うと自然言語処理における確率的なクラスタリング手法です。クラスタのことを「トピック」と読んでいます。
ある文書 ${d}$ の ${i}$ 番目の単語がトピック ${z}$ に属する、という形でクラスタリングします。
例えば、トピック 0 には「ホームランヒットスクイズ」など野球に関する単語が、トピック 1 には「ワールドカップ得点王オーバーヘッド」などサッカーに関する単語が頻出する、という結果が得られます。

どのトピックが選ばれるかについての確率(トピック分布の確率)と、そのトピック内での単語の選ばれやすさ(単語分布の確率)があり、それを見ることによって分析の概略を掴むことができます。

参考
Latent Dirichlet Allocation ゆるふわ入門 - あらびき日記
 Latent Dirichlet Allocations の Python 実装 - Mi manca qualche giovedi`?
Latent Dirichlet Allocation(LDA)を用いたニュース記事の分類 | SmartNews開発者ブログ

PDFからテキスト抽出

PDFファイルからテキストを抽出するのに、Apache PDFBox というライブラリを使用しました。
Apache PDFBox
https://pdfbox.apache.org/

使用方法はこんな感じです(公式より)。

java -jar pdfbox-app-x.y.z.jar ExtractText [OPTIONS] <inputfile> [Text file]

参考
https://pdfbox.apache.org/commandline/#extractText

楽にテキストを抽出できますが結構エラー吐きます。
また、出力されたテキストはPDFでの改行位置で文章が途切れているので、そこらへんをうまく処理する必要があるかと思います。

分析

テキスト抽出後、一度整形し、日本語のみを抽出し、形態素解析し、名詞だけをとりだして特徴量とし、LDAで分析します。
自分ではこんな感じで実験してみました。

主に機械学習関係の論文とスライドを462ファイル用意
特徴抽出前のPDFファイルは合計約628MB
特徴抽出後のテキストファイルは約3.7MB
LDAのトピック数は100、サンプリング回数は10000回
学習はおよそ26時間

実験結果はこんな感じになりました。
トピック分布の確率(のパラメータ)が0.1以上のトピックについて、頻出単語上位10個を表示しました。

Summarization:
	Topic num = 100
	print Topic if theta > 0.1 and 10 frequent words in Topic
Topic : 11 (theta = 0.5105679678472282)
	確率 : 0.025439009730502445
	モデル : 0.022912977793661367
	分布 : 0.02147939375233516
	データ : 0.01885995548985526
	学習 : 0.01504654071703569
	推定 : 0.014226189509251287
	関数 : 0.012995662697574684
	計算 : 0.009730502444809046
	問題 : 0.009628973829984244
	アルゴリズム : 0.007346610568722689
	状態 : 0.007196348218781981
Topic : 51 (theta = 0.12858576604531036)
	利用 : 0.025817941788200714
	評価 : 0.020462555889056332
	推薦 : 0.018718941875381416
	情報 : 0.017971678726663595
	アイテム : 0.015729889280510133
	システム : 0.01372473316478398
	データ : 0.012255115638972264
	ユーザ : 0.010598682325981094
	嗜好 : 0.007958352533844793
	検索 : 0.007385450786494464
	予測 : 0.005903378874870786
Topic : 77 (theta = 0.1504352870224158)
	言語 : 0.0222420226095673
	表現 : 0.016327894414434482
	意味 : 0.01551484100907724
	単語 : 0.015069332293812998
	パターン : 0.01056969426964415
	処理 : 0.010001670657682241
	翻訳 : 0.008453527872138999
	構造 : 0.007807540235005847
	解析 : 0.007729576209834605
	概念 : 0.007328618366096787
	参照 : 0.0066492175753188176
LDA completed.

今回用意した論文は半分くらいは統計的機械学習について、あとは自然言語処理、データマイニング、ニューラルネットワーク等となっています。
Topic : 11 は統計的機械学習に、Topic : 51 はデータマイニング(特に推薦)、Topic : 77 は自然言語処理に対応していると考えられます。
表示されてはいませんが、ニューラルネットワークに対応するトピックもあったので、用意したPDFファイルの傾向を掴めていると言っていいのではないかと思います。

実際には、自分の持っているPDFファイルを適当に突っ込んだので、分析結果が出たあとに何となく眺めてみて「確かにこんな感じだなー」と思いました。

感想

分析結果をどう活用するか

今回は分析して結果を見ただけですが、実際の分析結果を用いて、自分の興味のありそうな未読論文を推薦してくれるシステムとかが作れるかもしれません(Google Scholar のマイライブラリ等が使えそう?)。

プログラミング言語の使い分け

今回の試みとして、テキストの整形等はPythonやシェルスクリプト、計算の重い部分はJava、と役割分担をしてみました。

Javaでの機械学習の実装は面倒でしたが、Pythonでの実装より大幅に高速化されているのを確認しました(少なくとも倍近く)。
今回は26時間とかなりかかっていますが、サンプリング回数とトピック数が多いためであり、特にトピック数を減らせば計算時間が大幅に減らせます。トピック数が一桁だと数秒から数分でした(まあトピック数なんて事前にわからないんですけれども...)。
サンプリング回数はできるだけ多い方が良いと思います(本当はburn-inとかやらなきゃいけないんですがやってないです...)。
また、Javaに比べて手軽な処理やテキスト整形等はスクリプト言語であるPythonが便利でした。

結論として、前処理や特徴抽出に関しては、スクリプト言語で手軽に行うのが楽で良いと思います。
また、機械学習の手法に関しては、PythonやMatlab、Rで実装してみて、精度や計算時間を考慮してからC++やJavaで実装し直すのが良いのかな、と思いました。

データが大事

今回一番実感したのは、データの収集方法と、前処理、特徴抽出の大変さです。
PDFファイルからのテキスト抽出は結構ノイズが入るので、前処理でしくじると結果も悲惨なことになりました。正規表現やユニコードなど色々と勉強し直しました。

特徴抽出も、最初は全単語を用いていたのですが、収拾がつかなくなってしまったので、用いる品詞を限定することにしました。

今まで私は分析手法ばかりに目が行っていたのですが、データの収集や前処理、実験結果の分析なども同じ位大切ということだと思います。
そして分析手法とは違いあまり定式化されていないので、自分なりのアプローチを確立し、問題ごとに良く考える必要があると感じました。

2014-07-13

Pythonで主成分分析

Python 機械学習

概要

主成分分析(Principal Component Analysis, PCA)とは、

データの無相関化
データの次元の削減

を行う手法です。
簡単に言うと、データを分析しやすいように再構成し、可能なら次元を下げることです。

なぜ次元を削減する必要があるかと言うと、機械学習や統計において、データの次元が大きすぎると認識精度が悪くなる、次元の呪いという現象を回避するためです。
(2次元や3次元に変換できると可視化できる、というメリットもあります。)

今回は、Pythonを使って主成分分析を試してみようと思います。

主成分分析の例

ライブラリとしてscikit-learn、テストデータとしてiris datasetを用います。

scikit-learnはPythonの機械学習ライブラリです。主成分分析も実装されています。
導入等については、次の記事をご参照ください。
MacでPythonの機械学習環境構築(2014年5月版) - old school magic

iris datasetは、アヤメに関するデータセットです。
150個のデータがあり、3種類のアヤメがあります。がく片と花びらについて、それぞれ長さと幅を計測しているので、4次元のデータということになります。
詳しくはこちらをご参照ください。
Iris flower data set - Wikipedia, the free encyclopedia
UCI Machine Learning Repository: Iris Data Set

まずはデータを読み込みます。

import numpy as np
import matplotlib
import matplotlib.pyplot as plt

from sklearn import datasets

# データセットの読み込み
iris = datasets.load_iris()
X = iris.data
Y = iris.target

# 主成分分析前のサイズ
X.shape

Xは150個の4次元データなので、(150, 4)と出力されます。
これを主成分分析を用いて2次元に変換してみましょう。

# 主成分分析による次元削減
pca = decomposition.PCA(n_components = 2)
pca.fit(X)
X_pca= pca.transform(X)

# 主成分分析後のサイズ
X_pca.shape

変換後のデータはXは150個の2次元データなので、(150, 2)と出力されます。

各アヤメ(3種類)毎に可視化して見るとこんな感じになります。

f:id:breakbee:20140713182157p:plain

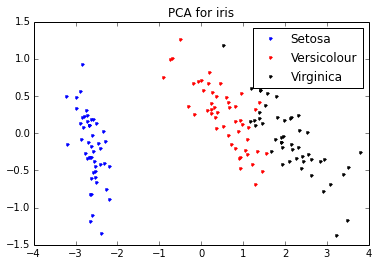
主成分分析のアルゴリズム

主成分分析が何をしているか、について簡単に説明します。
主成分分析のメインは固有値問題を解くことです。

固有値問題とは、ある行列 ${\bf{A}}$ について、
${\bf{Ax}=\lambda \bf{x}}$
となるような固有値 ${\lambda}$ と固有ベクトル ${\bf{x}}$ を求めることです。

元のデータを ${\bf{X}}$ 、データの次元を ${N}$ 、変換後の次元を ${M}$ とすると、

データの共分散行列を求める
共分散行列の固有値と固有ベクトルを求める
固有値が大きい順に、固有値と対応する固有ベクトルと並べ替える
(対応する固有値の大きい順に選んだ) ${M}$ 個の固有ベクトルを並べた行列 ${\bf{P}}$ を作る
データからその平均ベクトルを引いたデータを ${\bf{X_{bar}}}$ とする
データを行列 ${\bf{P}}$ を用いて変換する ( ${\bf{X_{pca}}=\bf{X_{bar}P}}$ )

となります。
先程、scikit-learnを使ってあっさりやっていた次元削減のコードは、次のコードに対応します。

### 主成分分析による次元削減

# 共分散行列を求める
X_bar = np.array([row - np.mean(row) for row in X.transpose()]).transpose()
m = np.dot(X_bar.T, X_bar) / X.shape[0]
# 固有値問題を解く
(w, v) = np.linalg.eig(m)
v = v.T

# 固有値の大きい順に固有値と固有ベクトルをソート
tmp = {}
for i, value in enumerate(w):
	tmp[value] = i

v_sorted = []
for key in sorted(tmp.keys(), reverse=True):
	v_sorted.append(v[tmp[key]])
v_sorted = np.array(v_sorted)

w_sorted = np.array(sorted(w, reverse=True))

# 次元削減
dim = 2
components = v_sorted[:dim,]
X_pca = np.dot(X_bar, components.T)

# 主成分分析後のサイズ
X_pca.shape

(実際には、scikit-learnの主成分分析は特異値分解と言う手法で主成分分析を行っています。)

参考:
【Python】主成分分析（PCA） - 音楽プログラミングの超入門（仮）
Python の数値計算ライブラリで固有ベクトルを求める - 備忘録として

どうして次元削減できるのか

主成分分析はシンプルなアルゴリズムです。
しかし、どうして固有値問題を解くと次元削減が出来るの？という疑問が残ります。
そもそも、固有値や固有ベクトルってどういう意味があるの？という方もいらっしゃるかと思います。

ここでは、ものすごくざっくりかつ不正確に固有値問題や次元削減の正当性について説明したいと思います。
ある1次元の変数 ${y}$ が、係数 ${a_{i}}$ と変数 ${x_{i}}$ によって表現されるとします。

${y = a_{1}x_{1} + a_{2}x_{2} + ... + a_{M}x_{M}} + ... + a_{N}x_{N}$

この時、 ${a_{i}}$ は大きい順に並んでいると思ってください。
さて、例えば ${a_{1}}$ が ${1000}$ 、 ${a_{2}}$ が ${500}$ といった大きい値なのに対して、 ${a_{M}}$ が ${1}$ 、 ${a_{M}}$ 以降がさらに小さい値だったとします。
この時、 ${y}$ は ${a_{M+1}}$ 以降を省いた

${y \simeq a_{1}x_{1} + a_{2}x_{2} + ... + a_{M}x_{M}}$

で近似することができます。要するに、係数が大きい変数が重要な成分(=主成分)で、係数の小さい変数( ${x}$ )は、どんな値をとっても結果( ${y}$ )に影響を与えないので無視しよう、ということです。

実は、この行列版が固有値問題と主成分分析です。
${y = a_{1}x_{1} + a_{2}x_{2} + ... + a_{M}x_{M}} + ... + a_{N}x_{N}$
を求めるのが固有値問題、係数 ${a_{i}}$ が固有値、変数 ${x_{i}}$ が固有ベクトルです。
つまり、固有値問題を解くことは、元のデータを分析しやすく再構成することにつながります。
そして、係数の小さい項を省いた部分が次元削減に対応しています。

より詳しいこと

上述した説明はあくまでもイメージなので、全然正確ではありません。
もし主成分分析について勉強したい、ということでしたら、次の2冊をおすすめします。

まず、固有値問題(線形代数)については、この本をおすすめします。

キーポイント線形代数 (理工系数学のキーポイント 2)

作者: 薩摩順吉,四ツ谷晶二
出版社/メーカー: 岩波書店
発売日: 1992/10/22
メディア: 単行本
購入: 5人クリック: 30回
この商品を含むブログ (26件) を見る

線形代数をイメージしやすく理解できるという点で、とても素晴らしい本だと思います。
(私が先程した固有値問題の説明は、この本の改悪でしかありません...)

そして、主成分分析の入門については、この本をおすすめします。

はじめてのパターン認識

作者: 平井有三
出版社/メーカー: 森北出版
発売日: 2012/07/31
メディア: 単行本（ソフトカバー）
購入: 1人クリック: 7回
この商品を含むブログ (4件) を見る

ここで述べた主成分分析はとても基本的な事項で、ここからカーネル主成分分析や部分空間法などに発展していきます。この本は、これらの事項を簡潔にまとめています。

補遺

今回のコードはgithub(というかiPython Notebook)で公開しています。
http://nbviewer.ipython.org/github/breakbee/PyNote/tree/master/

iPython Notebook があまりに便利で感動しています。

主成分分析のイメージの説明について、間違ってることや、こう説明したほうがいいよ、ということがありましたら、お知らせ頂けると幸いです。

2014-06-26

AnacondaがPython3に標準で対応しているので試してみました

Python

概要

AnacondaはPythonの機械学習ライブラリです。
Anaconda Scientific Python Distribution

Pythonの機械学習ライブラリだと、

numpy
scipy
matplotlib
scikit-learn
pandas

あたりが定番なのですが、Anacondaはここらへんをひとまとめにしてインストールしてくれます。個別にインストールするよりすごい楽です。iPythonとか便利ツールもインストールしてくれます。

そんなAnacondaなのですが、標準ではPython2系がインストールされるので、Python3系を使おうとすると少し面倒でした。

ですが、Python3.4に標準対応したAnaconda3が5月末にリリースされたので、そちらを使ってみようと思います。

Anaconda3

ここから対応するOSのインストーラをDLして実行します。
http://repo.continuum.io/anaconda3/

もしMacユーザであればpyenvを使うことをおすすめします。
前回の環境構築を参考までに。

scikit-learn のインストール

Anaconda3は(私が試した限り)標準でscikit-learnをインストールしません。
おそらく、ベースとなってるPython3.4と(pipを使ってpypiからインストールする時に)相性が悪い、ということだと思います。
詳しいことはこの記事に。
Python 3.4.0でscikit-learnがインストールできない？ - old school magic

この記事を書いた時に解決策のコメントを頂いていました。
pypiからではなく、gitから直接インストールすればOKです。
コメントを下さった方、ありがとうございます。

# Gitから直接インストール
pip install git+https://github.com/scikit-learn/scikit-learn.git

一応scikit-learnを使ったソースをいくつか試して見たのですが、ちゃんと動くことを確認しました。

2014-05-20

Python3でPyMCのインストール

Python 統計機械学習

概要

PyMCはPythonのベイズ統計用ライブラリです。特にMCMCに重点を置いています。
Python3にPyMCを導入するのに割りと手こずったのでメモします。
参考になれば幸いです。

インストールの前準備

今回はPyMC version 3を試します。(まだalpha版です。)
Python 2.7もしくは3.3に対応しています。

PyMC3
https://github.com/pymc-devs/pymc

依存しているライブラリは

Theano
NumPy
SciPy
Matplotlib

です。これらを事前にインストールします。

参考
MacでPythonの機械学習環境構築(2014年5月版) - old school magic

Theano

Anaconda(Python用の機械学習パッケージ)で一発です。
と言いたいところですが、Theanoでちょっと引っかかりました。

TheanoはDeep Learning用のPyhtonライブラリです。

Theano
http://deeplearning.net/software/theano/

PyMCでは計算時にTheanoの機能を一部使っているようです。

私の環境だと、theanoをimportしようとするとこんな感じのエラーがでました。
(エラーが出ない方はこの項を飛ばしてください。)

In [1]: import theano

The environment variable 'DYLD_FALLBACK_LIBRARY_PATH' does not contain the ... (Pythonのパス)
This will make Theano unable to compile c code. 
Update 'DYLD_FALLBACK_LIBRARY_PATH' to contain the said value, this will fix this error.

'DYLD_FALLBACK_LIBRARY_PATH'という環境変数を設定しろ、というエラーなのですが、設定してもうまく行かず困ってしまいました。
幸い同じようなエラーに遭遇した方がいらっしゃいました。

psycopg2, pymc, theano and DYLD_FALLBACK_LIBRARY_PATH - Stack Overflow
http://stackoverflow.com/questions/21713148/psycopg2-pymc-theano-and-dyld-fallback-library-path

TheanoのDevelopment版だとこの環境変数は必要ないとのことで、Development版を導入します。

# Development版をgitからインストール
pip install --upgrade --no-deps git+git://github.com/Theano/Theano.git

# 上のコマンドがダメならこちらのコマンドで
pip install --upgrade --no-deps git+git://github.com/Theano/Theano.git --install-option='--prefix=~/.local'

これでTheanoはOKです。

PyMCのインストールとテスト

PyMCをインストールします。

# gitからインストール
# 普通に pip install pymc してしまうとPyMC 2.3がインストールされてしまいますのでご注意を
pip install git+https://github.com/pymc-devs/pymc

PyMCのチュートリアルを試してみます。
PyMC 3 Tutorial
http://nbviewer.ipython.org/github/pymc-devs/pymc/blob/master/pymc/examples/tutorial.ipynb
同じ内容のスクリプトファイルはこちら
https://github.com/pymc-devs/pymc/blob/master/pymc/examples/tutorial.py

スクリプトの最後で図示しようとしているのですが、ここでもちょっとこけました。
(ここも環境によると思うので、エラーが出ないからは無視してください。)

In [10]: pm.traceplot(trace);

UserWarning: tight_layout : falling back to Agg renderer
  warnings.warn("tight_layout : falling back to Agg renderer")

Matplotlibのエラーみたいです。とりあえず図示結果を直接表示せず、画像に保存することで対処しました。

# こっちに書き換える
In [11]: pm.traceplot(trace).savefig("result.jpg")

これで一応動作確認終了です。

感想

前回から引き続き、この本の勉強の一環でインストールしました。

データ解析のための統計モデリング入門――一般化線形モデル・階層ベイズモデル・MCMC (確率と情報の科学)

作者: 久保拓弥
出版社/メーカー: 岩波書店
発売日: 2012/05/19
メディア: 単行本
購入: 16人クリック: 163回
この商品を含むブログ (19件) を見る

次は実際に動かしてみようと思います。
Theanoいじってみたいです。
iPython Notebook、かなり便利そうですね。

2014-05-13

Pythonで一般化線形モデル

Python 統計機械学習

概要

統計の勉強の一環で、最近はこの本を読んでます。かなり分かりやすいです。

データ解析のための統計モデリング入門――一般化線形モデル・階層ベイズモデル・MCMC (確率と情報の科学)

作者: 久保拓弥
出版社/メーカー: 岩波書店
発売日: 2012/05/19
メディア: 単行本
購入: 16人クリック: 163回
この商品を含むブログ (19件) を見る

統計モデリングに関する本です。一般化線形モデルを中心に話が進んでいきます。
この本はRを中心に話が進んでいきますが、せっかくなのでPythonで一般化線形モデルを試してみようと思います。

Pythonの統計ライブラリ

一般化線形モデルとは、線形回帰を(正規分布以外でも使えるように)拡張した統計モデルです。
詳しい説明は教科書に譲るとして、Pythonでのライブラリについてお話します。

Pythonで一般化線形モデル、というか統計全般のライブラリとして、簡単に調べたところメジャーなのが二種類あります。
scikit-learn と StatsModels です。

scikit-learn
http://scikit-learn.org/stable/index.html

StatsModels
http://statsmodels.sourceforge.net/devel/index.html

scikit-learn はどちらかというと機械学習の、StatsModels はどちらかというと統計のライブラリです。
今回はStatsModels を使ってみようと思います。

インストール

Anaconda入れるともれなくインストールされます。
Anaconda(というかPython)のインストールはこちらを。
MacでPythonの機械学習環境構築(2014年5月版) - old school magic

Pandasというデータ分析ライブラリも(データを読み込む時に)使います。
これもAnacondaに同梱されています。

使うデータ

先程紹介した本の著者である久保先生のデータをお借りします。
http://hosho.ees.hokudai.ac.jp/~kubo/stat/iwanamibook/fig/poisson/data3a.csv

どういったデータか簡単に説明すると、ある植物が種子を飛ばす数についてのデータです。
観測変数は3つあり、

y : 飛ばした種子の数
x : 植物の大きさ
f : 育てる時の肥料の有無(Cが肥料なし、Tが肥料あり)

です。種子の数について、植物の大きさや肥料との関係を調べます。
個体ごとに飛ばす種子の数の平均値が違うと仮定します。

先にネタバレしてしまうと、種子(y)と植物の大きさ(x)には関係がありますが、種子(y)と肥料の有無(f)は特に関係ありません。
肥料の有無はどちらかというと植物の大きさに関係してるので、確かに直感通りな結果ではあります。

一般化線形モデル

実際に関係を調べてみましょう。
天下りではありますが、fはyと直接関係のないデータなので、yとxの関係だけを調べます。
統計モデルとしてはポアソン回帰を用います。*1

数式で表すと、ある個体iが種子を飛ばす個数は、
${ \displaystyle p(y_i|\lambda_i) = \frac{\lambda_{i}^{y_i} \exp(-\lambda_i)}{y_i !} }$
に従うとします。ここで ${\lambda_i}$ は種子を飛ばす数の平均値で、

${ \displaystyle \log(\lambda_i) = \beta_1 + \beta_{2}x_i }$
と表されるとします。この ${\beta_1 , \beta_2}$ について推定します。

コードはこんな感じです。*2

import statsmodels.api as sm
import pandas

# PandasでCSVの読み込み
data = pandas.read_csv("data3a.csv")

# 植物の大きさ
x = sm.add_constant(data.x)
# 飛ばした種子の数
y = data.y

# ポアソン回帰
model = sm.GLM(y, x, family=sm.families.Poisson())
results = model.fit()

# 結果の表示
print(results.summary())

APIの詳細はこちら。
http://statsmodels.sourceforge.net/devel/glm.html
http://statsmodels.sourceforge.net/devel/generated/statsmodels.tools.tools.add_constant.html

一つだけ注意することがあって、sm.add_constant でxに定数列を加えないと、切片( ${\beta_1}$ )抜きで推定してしまいます。ここだけ何か腑に落ちないです。

結果はこんな感じです。

                 Generalized Linear Model Regression Results
==============================================================================
Dep. Variable:                      y   No. Observations:                  100
Model:                            GLM   Df Residuals:                       98
Model Family:                 Poisson   Df Model:                            1
Link Function:                    log   Scale:                             1.0
Method:                          IRLS   Log-Likelihood:                -235.39
Date:                Tue, 13 May 2014   Deviance:                       84.993
Time:                        11:39:50   Pearson chi2:                     83.8
No. Iterations:                     6
==============================================================================
                 coef    std err          t      P>|t|      [95.0% Conf. Int.]
------------------------------------------------------------------------------
const          1.2917      0.364      3.552      0.000         0.579     2.005
x              0.0757      0.036      2.125      0.034         0.006     0.145
==============================================================================

coefの列が推定値で、constが ${\beta_1}$ 、xが ${\beta_2}$ に対応しています。